【心理統計】代表値や尺度水準を知ろう！【超入門・基礎】

こんにちは、臨床心理士・公認心理師のしあんです。

今回も心理学関連の統計の基礎について説明していきます。

✓統計用語の意味がそもそも分からない
✓尺度って何…？

本記事は、文系で数学やら数字にアレルギー反応を起こす（筆者みたいな）人たちに向けた解決記事です。

数の分類基準である尺度水準の考えをきちんと理解すると、心理統計への理解もかなり深まるのでしっかり読んでおきましょう。

尺度が分かればその後の統計手法のヒントになります。

こんな人におすすめ！
・文系や心理学を学んでいて統計さっぱりな人
・統計に興味のある人
・尺度水準って何？な人
・統計の基本用語から学びたい人
・心理統計初心者
・数字アレルギーの心理学部生
※心理系大学院進学希望者は必須記事

まずは数について

そもそも数には決まった値の定数と値が変動する変数があります。

▼例
・定数…郵便番号や銀行コード、円周率3.14など固定の数
・変数…気温や人の体温、身長・体重など変わる数

↑こんな風に思いがちですが、統計をやっていくと「〇〇変数」などいろいろな用語が増えるので、個人的にはちゃんと把握するのがおすすめ。

基本的に心理統計で扱うのは変数で、変数は量的変数と質的変数の2つがメジャーです。

量的変数と質的変数とは

量的変数は計算目的、質的変数は分類目的の数を指します。

後に出てくる間隔尺度と比率尺度は量的変数で計算が可能、名義尺度と順序尺度は質的変数で計算できず分類メインな変数です（尺度についてはこちら）。

おおまかな数の特徴を知るー代表値ー

代表値とはデータ全体の中心的な特徴を把握する値で、下記3つがメジャーです。

・最頻値（モード）
・中央値（メジアン）
・平均値（アベレージ）

▼例題：6人のテストの点数
56、70、65、62、59、62

例題を見ながら3つの代表値について簡単に紹介しますね。

最頻値（モード）

最頻値は、データの中で現れた回数（度数）が一番多い値です。

▼例題：6人のテストの点数
56、70、65、62、59、62

例題でいけば「62」が1番多い＝最頻値。

中央値（メジアン）

中央値は数を小さい順に並べたとき真ん中にくる数で、中央値が2つある場合（データが偶数の場合）は2つの平均が中央値です。

▼例題：6人のテストの点数
56、59、62、62、65、70

今回は（62＋62）÷2=62が中央値ですね。

平均値（アベレージ）

平均値はご存じの通り、データ全てを足して個数で割った値です。

▼例題：6人のテストの点数
56、70、65、62、59、62

（56＋70＋65＋62＋59＋62）÷6=62.33

≒62点が平均値ですね。

例題を少し変えてみますが、（30＋96＋65＋62＋59＋62）÷６=62.33≒62点でも平均は同じに。

ちなみに勉強苦手な1人を加えてみます。

（3＋70＋65＋62＋59＋62）÷6=53.5点になり、平均も6人の出来の良さ（印象）もちょっと下がりますね…。

代表値の特徴とイメージはこんな感じ。

代表値	特徴
最頻値	あまり役立たないけど外れ値に強い
中央値	真ん中は分かるけど全データを見れない
平均値	全データ見れるけど外れ値の影響大

平均値は外れ値に引っ張られやすいことと、どの代表値もデータが少ないとあまり意味がない点は知っておきたいところ。

数の意味分けー尺度水準ー

数についての用語説明をしたところで、具体的にみていきます。

同じ「1」「2」「3」という数でも、下記のように数の意味や性質はそれぞれ違います。

・郵便番号の「123-」
・順位の「1位」「2位」「3位」
・温度の「1℃」「2℃」「3℃」
・重さの「1㎏」「2㎏」「3㎏」など

数の意味や性質に沿って数を分類する基準を尺度水準と言い（by S.S.スティーブンス）、４つの尺度に分類可能です。

・名義尺度
・順序尺度
・間隔尺度
・比率尺度

統計処理する際は比率尺度が一番幅広く処理ができ、名義尺度に近づくほど統計処理はしづらくなります（ただの分類になっていく…）。

名義尺度

名義尺度は順番や大小関係などがなく、ただの分類記号としての数です。

・男を「1」女を「2」としてデータ分けする
・郵便番号の「123-」
・背番号　など

順序尺度

順序尺度は、数字間の等間隔性はないものの順序や大小関係のある数です。

・成績や順位の「1位」「2位」「3位」など

等間隔性についてですが、たとえば「1位」と「2位」の間と、「2位」と「3位」の間って等間隔ではないですよね。

一方、たとえば1分は必ず60秒なので時間の分単位の間隔は等しいため、その場合は等間隔と言えます。

間隔尺度

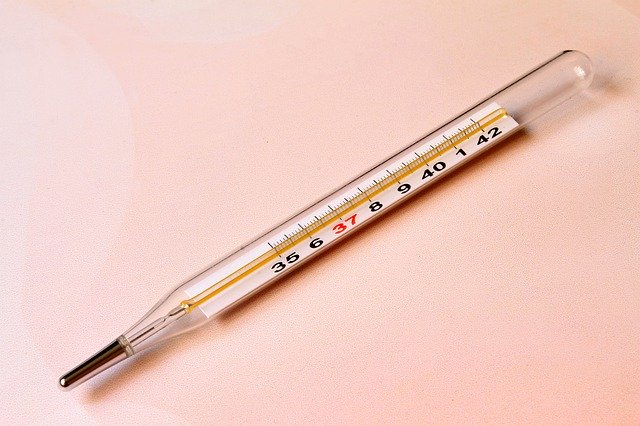
間隔尺度は順序も等間隔性もあり、ゼロ（原点）がない数です。

・時刻
・温度の「1℃」「2℃」「3℃」
・日付け　など

たとえば温度の「0℃」は絶対的な原点ではないので間隔尺度に分類されます。

比率尺度

比率尺度（比例尺度）は順序も等間隔性もゼロ（原点）もある数です。

・長さ
・重さの「1㎏」「2㎏」「3㎏」
・お小遣い　など

おわりに：代表値や尺度水準はおおまかなデータ把握方法！

数とその分類については、具体的な統計話に入る前に知っておくべき前提知識です。

変数には計算できる量的変数と分類メインの質的変数があり、データの大まかな特徴を捉えるには3つの代表値があります。

代表値	特徴
最頻値	一番多く出現するデータ。あまり役立たないけど外れ値に強い
中央値	順に並べたときの真ん中データ。真ん中は分かるけど全データは見れない
平均値	総和÷データ数。全データ見れるけど外れ値の影響大

代表だからといって1つの見方・データで特徴を把握すると、外れ値を考慮しないなど危険があるので注意。

「何でも平均でいいでしょ？」と思っている人は一旦考えを改めましょうね！

また、数の意味や分類は4つの尺度に分けられます。

尺度水準	順序	大小関係	等間隔性	ゼロ（原点）
名義尺度	×	×	×	×
順序尺度	〇	〇	×	×
間隔尺度	〇	〇	〇	×
比率尺度	〇	〇	〇	〇

参考資料

割と本格的な内容をマンガでゆるく解説しているのがこちら。

心理統計に限らず、統計知識が必要な人全般におすすめな1冊です（アレルギー起こす人にマンガ本は本当にありがたい…！）。

そもそもな基本話が多いので、みなさんの「でもさぁ…？」って疑問が載っていて解消されるので是非。