【心理統計】相関の基礎｜相関係数や因果関係との違いもざっくり解説

こんにちは、臨床心理士・公認心理師のしあんです。

今回は相関の概要についてざっくり解説します。

✓相関がよく分からない
✓相関関係と因果関係の違いがいまいち
✓統計や数字が嫌いな文系・心理の民

特に、相関＝因果と思っている心理系大学院受験生や心理学部の民は本記事を要チェックです。

そうでない人でも、統計を扱う人や興味ある人は参考にご覧ください。

こんな人におすすめ！
・相関についてよく分からない人
・統計に苦手意識がある人
・小難しい本や数式が苦手な人
・相関の特徴をざっくり抑えたい人
※心理系大学院受験生は必須

相関と散布図とは

相関（correlation）とは、2つの変数（データ）の関連性のことです。

関連性というのは「背が高い人ほど体重が多い」ような、片方の変数（x）が大きくなったときにもう片方の変数（y）が変化する状態を指します。

また、散布図（scatter plot）は縦軸と横軸で2つの変数の関連性を捉えるグラフです。

散布図を見ると相関関係をぱっと見で理解しやすくなるメリットのほか、変数（x）からもう片方の変数（y）を予測したいときに役立ちます。

相関関係と因果関係の違い

相関関係は2つの変数（データ）の関連性で、因果関係とは原因となる独立変数があって結果という従属変数に関係していることです。

他にも、たとえば「牛乳を多く飲むと背が伸びる」という相関関係があったとしても「牛乳を飲む（原因）から背が伸びる（結果）」という訳ではありません。

「たくさん寝たから」「栄養ある食事をしっかり摂ったから」といった原因も考えられるため、相関関係がある＝因果関係があるとは言い切れないということを覚えておきましょう。

相関関係はあくまで関連性があることを示すので「傾向がある」程度、因果関係は原因→結果という強い結びつきがあります。

相関の3種類

相関は大きく3つのタイプに分けられます。

散布図にして見ると相関を捉えやすくなるため、相関を調べるときは視覚化するようにしましょう！

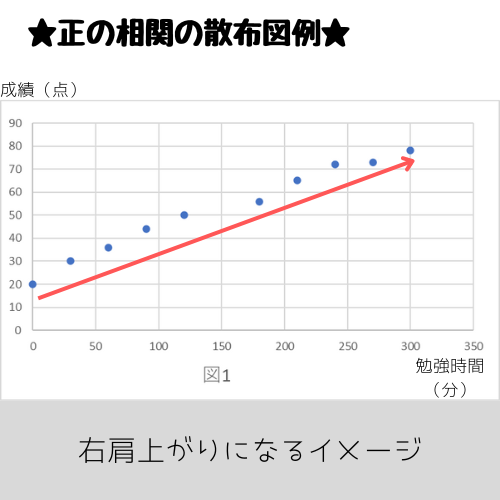
正の相関

正の相関は、片方の変数（x）が大きくなると、もう片方の変数（y）も大きくなるような関連性を指します。

▼例
・勉強時間が増えると成績が上がる

散布図で見ると右肩上がりのグラフになるのが特徴。

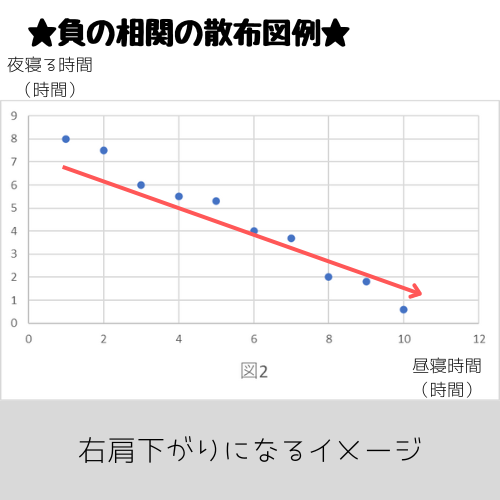
負の相関

負の相関は、片方の変数（x）が大きくなると、もう片方の変数（y）が小さくなるような関連性を指します。

▼例
・昼寝時間が増えると夜眠れなくなる

散布図で見ると右肩下がりのグラフに。

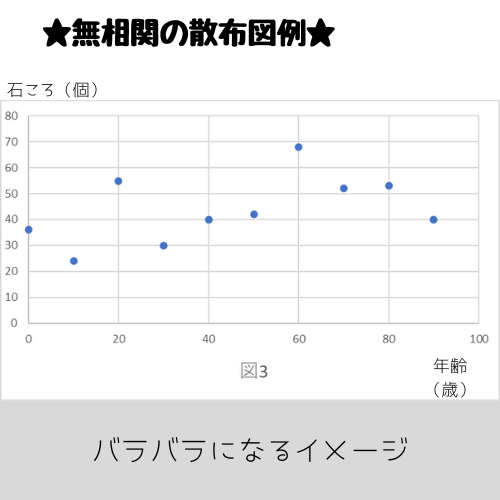
無相関

無相関は、変数（x）がどう変化しようともう片方の変数（y）に影響を表さない（無関連）状態を指します。

▼例
・年齢とその辺に落ちている石ころの数など

散布図にするとまとまりのない、バラバラな様子に。

本当は弱い相関があっても反例を多く挙げて無相関と決めつけないように気をつけましょう（無相関であって欲しい主観に囚われないように、データは客観視しましょうね^^）。

相関係数とは

相関係数（correlation coefficient）は、2つの変数（データ）間の相関関係の強さや方向性を示す統計量で、よく「r」と表記されます。

相関係数の範囲は－1.0～＋1.0で、マイナスは負（散布図は右肩下がり↘）、プラスは正（散布図は右肩上がり↗）、0は無相関を示します。

相関係数（r）の範囲	相関の強弱
r＝0	無相関
r＝±0.2以下	ほとんど相関ナシ
r＝±0.2～±0.4以下	弱い相関
r＝±0.4～±0.7以下	中等度の相関
r＝±0.7～1.0以下	強い相関

また、相関係数はたとえばr＝0.2とr＝0.4で2倍、r＝0.2とr＝0.8で4倍のような倍数の関係はありません。

r＝0.2とr＝0.4の差（0.2）と、r＝0.6とr＝0.8の差（0.2）に等しさ（等間隔性）もありません。

また、変数（x）と変数（y）に高い相関係数が出た＝相関アリとすぐに決めつけられるわけではなく、第三の変数（z）による疑似相関の可能性もあります。

▼疑似相関
2つの変数に実際は相関がないものの、他の要因で見かけ上では相関がみられること。
例：サプリ（変数x）を飲めば1ヶ月で－5㎏（変数y）達成可能！
→サプリと－5㎏の効果に直接的な関係はなくて「毎日30分の運動」「栄養バランスを整えた食事管理」など他の要因（変数z）が絡んでいる

こういった相関係数の性質を知ると「ただ数値を見れば相関関係が分かる」という訳ではないのが分かりますね。

代表的な相関係数には、ピアソンの積率相関係数、スピアマンやケンドールの順位相関係数があります。

※具体的な計算式も必要かもしれませんが、数字アレルギー回避のために本記事では省いて概要だけ紹介します

ピアソン（Pearson, K）の積率相関係数

積率相関係数とは、対象となる変数（x・y）が間隔・比率尺度の場合（どちらも量的変数＝計算できる場合）に使える相関係数で、ピアソンのものがかなりメジャー。

尺度について復習したい人は下記記事も参考にしてください！

ピアソンの積率相関係数を利用する場合は、散布図でデータを見て、変数（x・y）に直線的な関係があるかを先に確かめておきましょう。

パラメトリック（データが正規分布を仮定する場合）で利用なのもポイント。

＼　正規分布忘れた人は要復習　／

スピアマン（Spearman, C）・ケンドール（Kendall, M）の順位和相関係数

順位相関係数は、対象の変数（x・y）が順位尺度の場合に用いる相関係数で、スピアマンやケンドールのものが有名です。

順位相関係数を利用する場合は、ノンパラメトリック（データが正規分布しない場合）で用いるのがポイント。

外れ値のあるデータにも対応可能というと積率より順位相関係数の方が万能のように聞こえます…

が、順位相関係数はあくまで扱うのは順位データであって、各変数間がどれだけ離れているかなど詳細さに欠けてしまうデメリットもあります。

積率・順位の相関係数を利用するためには、データの性質を確認し、散布図で視覚的に見ておきましょう。

おわりに：相関は散布図チェックで関連性を見よう！

相関とはあくまで変数（x）と変数（y）の関連性を調べる方法で、散布図にすれば大まかな相関を見ることも可能です。

相関を量る相関係数でメジャーなもの＆特徴は下記の通り。

相関係数	代表	対象の変数	利用ポイント
積率相関係数	ピアソン	間隔・比率尺度	パラメトリック データが正規分布仮定
順位相関係数	スピアマン・ケンドール	順位尺度	ノンパラメトリック データが正規分布仮定しなくても可

相関は外れ値の影響を受けやすいので、数値だけで判断せず、散布図でも確認することがかなり重要です。

出てきた相関係数が本当に意味のある数値なのかを確認するためにも「外れ値があるか」「直線的/曲線的な相関があるか」くらいは目視しましょう（考察のヒントにもなるぞ！）。

相関があるからといって因果関係があると飛躍しないようにも気をつけましょうね。

さいごに

長くなりましたが、最後に参考書も紹介するので心理系大学院を目指す人は参考にどうぞ。

＼心理統計をざっくり勉強するなら／

＼丁寧な解説で勉強したいなら／

1冊目はド定番で簡潔、2冊目はいきなり統計初心者が読んでもハードル高いと思いますが、数学に抵抗ない人や多少は数学出来る人ならかなり読みやすいかと。

「統計」ってだけで敬遠するのが一番よろしくないと思うので、読みやすい方から向き合ってみましょう。