こんにちは、臨床心理士・公認心理師のしあんです。
卒論を書く心理学部生や心理系大学院進学者にとっての鬼門・心理統計。
心理統計って「そもそも何言ってるのか分からない」という抵抗が強いだけでなく、多少勉強しても「どんなときにどの統計手法を使えばいいのか分からない」という難しさがあります。
✓統計用語少しは覚えたけどまだ分からん
✓パラメトリック検定とノンパラメトリック検定の違いって何?
✓t検定だけ分かればいい?ダメ?
✓t検定の対応のあるなしって何?!
✓正規分布ってどゆこと?
今回はパラメトリック検定とノンパラメトリック検定の違いやそれぞれの統計手法の特徴、正規分布についてざっくり要点を解説します。
上記の悩みがある人は是非参考にしてみてください!

迷える子羊シリーズ
こんな人におすすめ!
・心理統計アレルギーの人
・卒論(修論)でどの統計手法使えばいいか分からない人
・パラメトリック検定とノンパラメトリック検定が分からない人
・正規分布の特徴をよく分かっていない人
・心理学部生
※心理系大学院受験生は必須
\ 復習すると理解度ダンチだぜ /
正規分布(normal distribution)とは
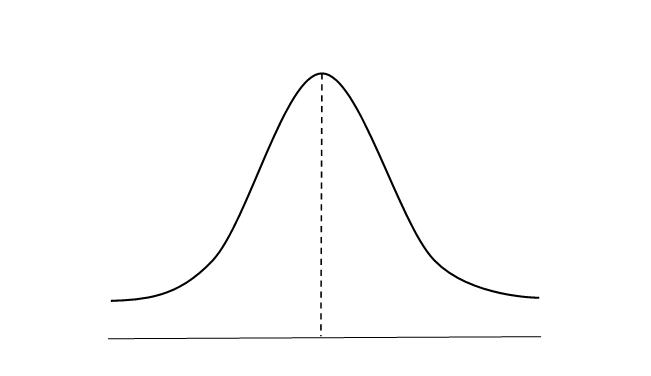
正規分布とは、同じ条件でデータを取ってグラフ化した際に①平均値周辺がもっとも大きくなり、②平均値周辺を中心に左右対称にデータが小さくなる分布で、いわゆる釣り鐘型の分布を指します。

↑画像みたいなやつね
数学者のガウスが見出した背景があり、ガウス分布と呼ぶこともある
学校のテストの点数やサイコロを振った出目の確率、男女の身長の平均など、実は世の中には正規分布するデータや現象が多くあるとか。
たとえば、男性の身長平均が170cmとして、平均周辺の身長の人が多くて160cm以下や180cm以上は少なく感じていきますね。

不思議だよね
サイコロの出目のような確率も、案外試行回数を増やしていくと何十回連続で同じ数が出るのはあり得ない!とか。
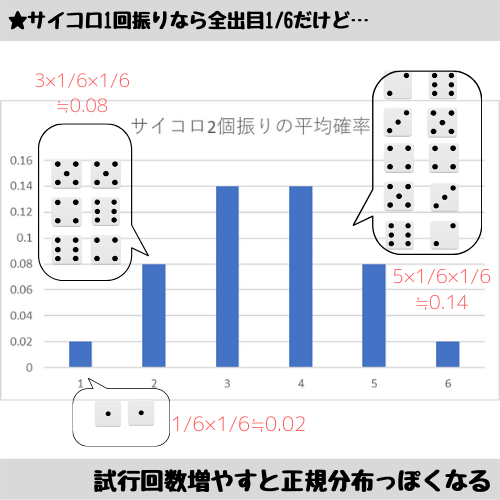

(あ、縦軸が確率、横軸が2個振りで出る数の平均値です)

何故か確率は収束してゆくのだ
社会や全データという母集団から1人・1回・1個のデータを見てもただの確率でしかありませんが、母集団から抜き出すデータ数が多いほど正規分布に似る現象は中心極限定理と言います(用語覚えなくてもいいけどこの性質は知っておこう)。
正規分布の特徴はこんな感じ。
✓釣り鐘のてっぺん(中心)は平均値=中央値=最頻値
✓標準偏差が小さいと高い(尖った)釣り鐘型、標準偏差が大きいと低い(ゆるやかな)釣り鐘型になる
✓平均±1標準偏差に全体の約68%のデータが含まれる
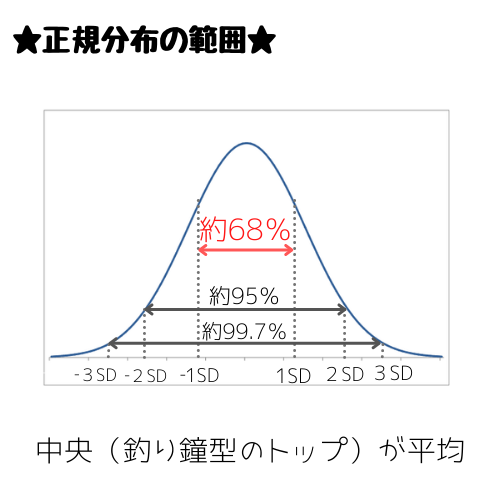
±2SDの範囲には全体の約95%、±3SDの範囲内なら全体の約99.7%が含まれると考えられます。
全データ(母集団)が正規分布するのであれば、標準偏差という平均からのばらつきの中のおおよそのデータ数を推測することができます。
▼例:
成人男性の身長平均が170cm、標準偏差が5とすると、±1SDなら全体の68%が身長165cm~175cmということになる
元のデータの性質を推測できるということは、偏差値なら平均=50、標準偏差=10として±1SD=40~60として学力を測定したり、身長なら服の標準サイズの参考にしたりなど役立てることが可能です。
知能検査のIQ測定も平均=100、標準偏差=15として正規分布を仮定している
ちなみに、正規分布は平均と分散(標準偏差)によってグラフの形を変えますが、平均が0で分散が1のデータを標準正規分布と呼びます。

正規分布の話は一旦ここで終えます
【最低限の】正規分布
・平均を中心に左右対称の釣り鐘型になるグラフ分布
・平均±1SDに全体の約68%が含まれる
心理統計の手法


正規分布で頭疲れた人は一旦ブラウザバックして休もう!

(これ以降(英語名)検定たくさん出るけど全部は覚えなくていいよ)
さて、卒論や修論で研究するにあたって心理統計はまず欠かせません。
男女差や、実験群と統制群(実験してない群)の差を調べたいとき、心理統計には
この2種類があります。
心理統計が難しい理由の1つって、研究に対してどの統計手法を使えばいいかさっぱり分からないことだと思います。

筆者「はー-い(白目)」
パラメトリック(parametric)とは「パラメーター(parameter:母数)によること」という意味なので、検定対象の母集団がパラメーターで規定できるのか=正規分布するのか・しないのかという違いがあります。

釣り鐘型になるだろう集団のデータを扱うか否かね
パラメトリック検定とノンパラメトリック検定の特徴や違いについてざっくり解説するので、意味不明な人は最後までもう少し勉強しましょう。
パラメトリック検定(parametric test)
パラメトリック検定は、母集団がパラメーターで規定できる=正規分布していることを仮定した統計手法を指します。
また、等分散性(:分布が左右で等しく分散しているか)があるかどうかによってパラメトリック検定の種類は変わってきます。
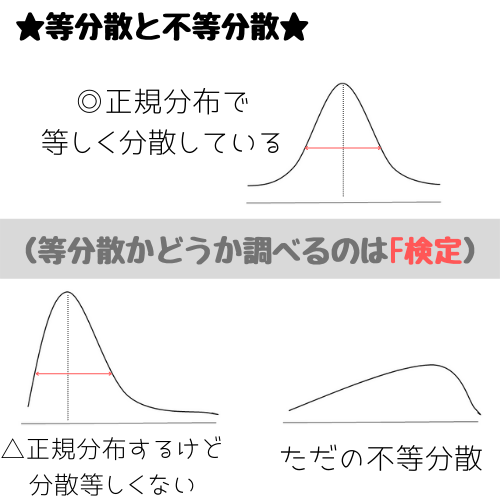
等分散性を調べるにはF検定を利用する。等分散でないならWelch法(やMann-Whitney検定)を採用する。※多重性(検定を繰り返すことで)の問題があるためF検定を飛ばす考えもあり
正規性(母集団が正規分布するのか)を確認するための事前検定としてShapiro-Wilks検定やKolmogorov-Smirnov検定もあるが、これもやはり多重性の問題で有意水準に影響が出る恐れあり
パラメトリック検定で扱うのは平均や標準偏差で、間隔・比率尺度のデータを扱うことが多いです。
\ 尺度って覚えてる? /
代表的な統計手法は、2群の差の比較ならt検定、3群以上の差の比較なら分散分析(ANOVA)。

みんな大好きt検定はパラメトリックゥゥウ!
ノンパラメトリック検定よりも精度は高い特徴がありますが、データ数が少ないと使えないため注意。

データ数が少ないとそもそも正規分布を描けないね
【統計やる人はもう少し】t検定の「対応あり」と「対応なし」?
いざt検定をしようとすると「対応のある」「対応のない」の2パターンが出てきて困る人もいるので(筆者)、違いをざっくり解説しておきます。
「対応のある」→同じサンプルからデータを得る場合(例:A群のベースの体重と、1ヶ月後のA群の体重の比較)
「対応のない」→違うサンプルからデータを得る場合(例:統制群と実験群のベースの体重の比較)

みんな大好き「男女差」は対応がない方だね
対応があるならそのままt検定を使って、対応がない場合は(最近は等分散or不等分散関係なく)Welch法を使うのが多め。
パラメトリック検定は、検定したい母集団が正規分布していると仮定する統計手法
・「対応あり」で等分散→t検定
・「対応なし」→(F検定+)Welch法が多め
ノンパラメトリック検定(nonparametric test)
ノンパラメトリック検定は、母集団がパラメーターで規定できない=正規分布しないと仮定した統計手法を指します。

母集団の分布は問わないよ
パラメトリック検定と違ってデータ数が少なくても適用できるため使いやすいのが特徴。
ただし、パラメトリック検定よりも精度は劣るのと、パラメトリック検定が使える場合にノンパラメトリック検定を使うと精度が落ちるデメリットがあります。

何でもノンパラ使うんじゃなくてちゃんと見極めようね
ノンパラメトリック検定で扱うのは順位平均や大小関係、中央値で、名義・順序尺度のデータを扱うことが多いです(正規分布しない間隔・比率尺度も)。
代表的な手法はこんな感じ(本記事での詳細は割愛!)。
▼名義尺度に使う
✓カイ二乗検定(治験薬Aと治験薬Bの効果差を見るなど2群の差やズレをみる)
▼2群の比較をする
✓Wilcoxon rank sum testやMann-WhitneyのU検定(中央値の差をみる。どちらもWelch法のノンパラ版というイメージ。パラメトリック検定でいう対応なし版)
✓Wilcoxon signed rank test(上記の対応あり版)
▼3群以上を比較する
✓Kruskal-Wallis test(中央値の差をみる。対応なし版)
✓Friedman検定(上記の対応あり版)

院進学希望者は覚えよう。そうじゃない人は卒論で使う以外忘れて良し!
3群以上の比較で有意差があったときは、多重比較で具体的にどこに有意差があったかを調べるのはお約束。
ノンパラメトリック検定は、検定したい母集団が正規分布しないと仮定=どんな分布でもサンプルが少なくても使える統計手法
おわりに:正規分布を仮定するかは統計選択の基本

正規分布にはこんな特徴があります。
・平均を中心に左右対称の釣り鐘型になるグラフ分布
・平均±1SDに全体の約68%が含まれる
身長・体重の平均など不思議なことに世の中正規分布することは多く、心理統計では正規分布を仮定した研究は多いです。
正規分布を仮定する統計手法をパラメトリック検定、正規分布を仮定しない統計手法をノンパラメトリック検定と分けます。
統計手法の選択パターンはこんな感じ。
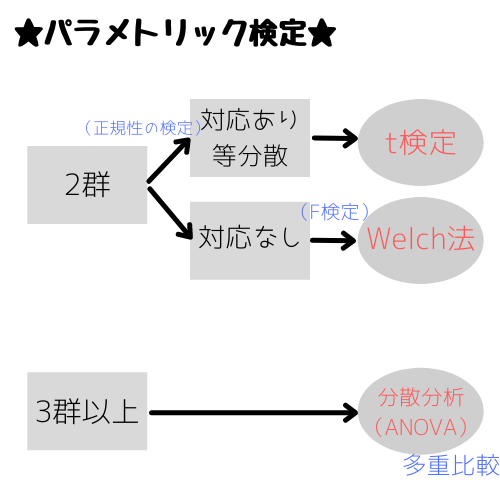

同じサンプル対象が「対応あり」で、男女差とか別サンプル対象が「対応なし」だったな
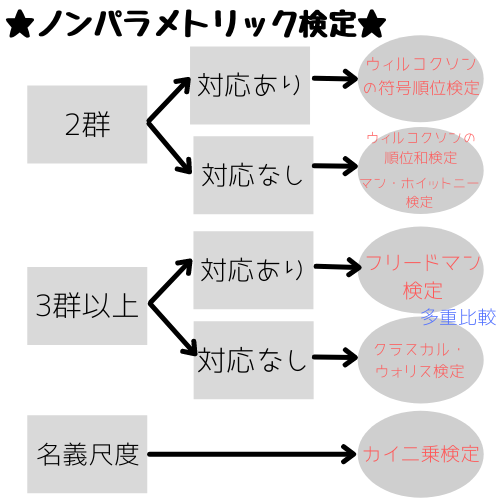

統計何使えばいいか分からない人は参考にどうぞ
パラメトリック検定で正規分布を確認するために正規性の検定、等分散を仮定するためにF検定といった事前検定も確かにあります。
が、同じデータに対して何度も統計処理をすると多重性の問題で有意水準に影響が出る恐れもあるため注意。

何事も必要最低限に◎
基本的にノンパラメトリック検定の方が気軽に使えますが、パラメトリック検定の方が精度は高いです。
また、パラメトリック検定が使える条件でノンパラメトリック検定を使ってしまうと、第2種の誤り(帰無仮説を棄却できるのに採用してしまうこと。本当は有意な結果なのに有意じゃないとしてしまうこと)が生じやすいデメリットもあります。
それなりにデータ数があって、平均や標準偏差を扱う間隔・比率尺度で、正規分布を仮定しそうな場合はパラメトリック検定を使っていく方が良いかもしれません。

勉強お疲れ様!統計選んだらあとはソフトで計算じゃ()
参考資料
・これから心理統計を勉強予定の人
・ブログじゃなくて本を手元に置いていつでも見たい人
・正規分布やパラメトリック・ノンパラメトリック検定、その他の基礎も復習したい人
そんな人はこちらをどうぞ。
\ 大体の人が持ってる /
B5くらいで意外とでかく、文字がびっちりなので、初見では「ウッッ」と抵抗感じるかもしれません(by筆者)。
が、とにかく基礎の説明を何度もしてくれるので土台作りにはおすすめ。

筆者数字も文字もダメなんかい
院試対策も兼ねていて、一般学部生(?)には手を出しづらいかもですがこちらも分かりやすいです。
上の「よくわかる」シリーズより小さくてイラストも多いので、勉強アレルギーな人におすすめ。
心理統計の概要を最低限説明しているので、これ読んで他の心理統計本読むと理解しやすいかと。
最低限の理解なので、細かく知りたいって人には向かないと思います。

以上!解散ッ!










コメント