こんにちは、臨床心理士・公認心理師のしあんです。
心理学を勉強している学生にとって、心理統計で最初に標準偏差（SD）でつまずく人は多いですね。
✓標準偏差が大事っていうけど何なの？（泣）
✓分散とどう違うの？
✓平均じゃだめなの？
卒論や修論にも関わる超重要用語なので、標準偏差（SD）が分からないと研究も論文も進みません…。
今回も超基礎編で、平均や分散、標準偏差（SD）についてざっくり解説します。
詳細に解説しても文系にとっては鬼門なだけだと思うので、参考書よりもコンパクトにいきます！
本記事すっぽかすと今後の心理統計詰むレベルの基礎編
用語は多いけど覚えよう…！
心理学部の統計講義や卒論で苦戦する人や、文系で統計を扱う人で「数字が苦手」なら必読です。
こんな人におすすめ！
・文系や心理学を学んでいて統計さっぱりな人
・標準偏差でつまずいている人
・統計に興味のある人
※心理系大学院進学希望者は必須
心理統計で必要な「統計の考え方」
「そもそも心理学と統計にどんな関係があるの？」と思いますよね。
心理学は、心という客観的なデータを科学的に証明していく学問なので、概念を客観視する指標として数字（統計）はうってつけなんです。
「イライラする」と言っても人にはどの程度か伝わりませんが、「10点満点中8点くらいイライラしている」ならイライラ具合をかなり共有しやすいですね。
こんな風に一般的に分かりやすくするために統計を扱いますが、統計本でよく見るシグマ（Σ）などの式が複雑なため挫折しやすいです…。
ムリ
大きな声では言えませんが、心理統計を学ぶ上で複雑な式を覚えたり、計算する力は不要です。
（太字使ってるやん）
①標準偏差などの用語、②SDなどの略語、③それぞれを求めて何を知りたいかを知るだけで卒論や修論には十分太刀打ちできるため、式より用語や意味など考え方をしっかり理解しましょう。
式は機械がやってくれるから、数値から情報を読み取れるようになろう
まずは『平均（mean）』のおさらい
多くの人が知っているように、平均（mean）は全データの総数を個数で割った値ですね。
▼平均の例
仲良し中学生5人のテストの点数（56、78、64、59、62）
（56＋78＋64＋59＋62）÷5（人）＝63.8点≒64点が5人の平均点
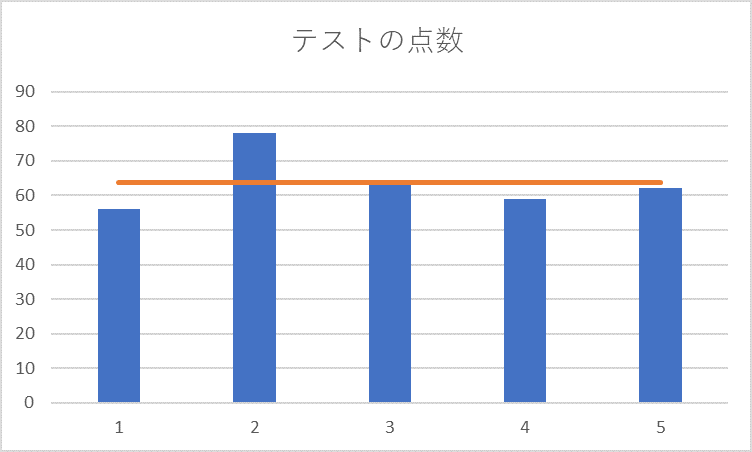
平均は、全データを考慮しておおよその中心を知る値というイメージ。
平均値は代表値の一種だね
全データを考慮して平均的な値をみれるとだけ聞くとすごく便利な指標ですが、極端な数値（外れ値）の影響を受けやすいデメリットがあります。
平均値を参考にする際は、元のデータ内容に偏りがないかを確認しましょう（正規分布については別途記事化）。
『偏差（deviation）』と『分散（variance）』
「標準偏差がよく分からない！」と言う人はその前段階にある『偏差』と『分散』の理解が怪しい人が多いので1つずつみていきましょう。
『偏差』は、各データから平均を引いた差のことです。
▼偏差の例
仲良し中学生5人のテストの点数（56、78、64、59、62）
平均：64点
偏差=各データ－各平均
①56－64＝-8
②78－64＝14
③64－64＝0
④59－64＝-5
⑤62－64＝-2
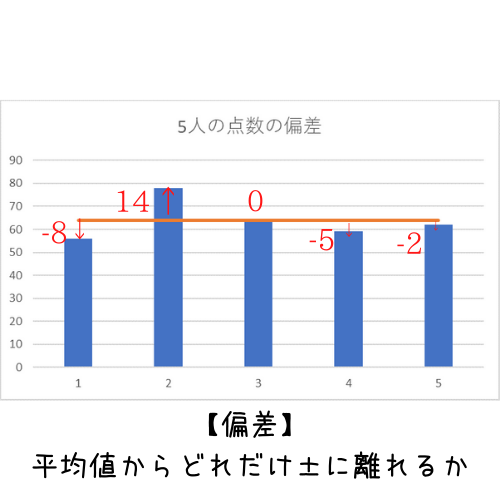
偏差はそれぞれのデータが平均からどれほど離れているかを意味します。
平均よりも個々のデータに注目した考え方ですね。
プラスもマイナスもどっちもあるよ
そして、それぞれの偏差を2乗して合計したら平方和になり、平方和をデータの個数で割ったものが『分散』です。
分散では各データのばらつきをみることができます。
ついてこれてるか？
式覚えなくていいから考え方だけ分かるといいな！
▼分散の例
仲良し中学生5人のテストの点数（56、78、64、59、62）
平均：64点
偏差：-8、14、0、-5、-2
★偏差²の総和（平方和）
＝(-8²)＋(14²)＋(0²)＋(-5²)＋(-2²)
＝64＋196＋0＋25＋4
＝289
★分散＝偏差²の総和（平方和）÷データの個数
289÷5（人）＝57.8≒58
んん？Q：偏差も分散も各データのばらつきで似てない？
偏差だとプラスマイナスのどちらもとれるため、足し引きした際にゼロになる可能性があります（ゼロになっちゃったら詳しくデータ見れないね）。
そこで、ゼロになるのを防ぐために偏差の2乗の平均（分散）を求めることで、各データのばらつきをしっかりみれるようになります。
偏差よりも分散の方が精度が高いんだね
ちなみに、2乗したら情報によっては「cm→cm²」など単位が変わってしまう恐れもあるので分散だけでは不十分。
分散でも不十分なんかーい！
分散よりも万能な値が標準偏差です。
分散が分かれば標準偏差の出し方も分かりやすいのでついでに知っておきましょう！
標準偏差（SD：Standard Deviation）
統計を扱う人なら絶対に聞くのが標準偏差（SD）です！
標準偏差もデータのばらつきを知る指標で、標準となる偏差（各データが平均からどれほど離れているか）という意味。
「平均」偏差ではないんだね
統計判定でよく見聞きする2SDは標準偏差の2倍の値ということで、統計的にもかなり有効な値になってきます。
統計本などでこんな式を見かけてやる気失せる人は多いと思いますが、
別にこの式は覚えなくて問題ないので無視しましょう。
標準偏差は√分散（分散の平方根）で求められます（分散は標準偏差の2乗ですね）。
√（ルート）をつけることで、分散で単位がずれてしまっても戻すことが可能（らしい。数学分かる人なら分かるはず）。
▼標準偏差の例
仲良し中学生5人のテストの点数（56、78、64、59、62）
平均：64点
偏差：-8、14、0、-5、-2
分散：58
標準偏差＝√58＝7.61577311
【悲報】筆者、数学できません
関数電卓使うかググればおｋ
標準偏差は、平均値ではみえてこない全データの散らばり具合を知ることができるのが特徴的です。
平均値だけだと、たとえば同じ平均＝63.8点でも個々のデータのばらつきが違うことがありえます。
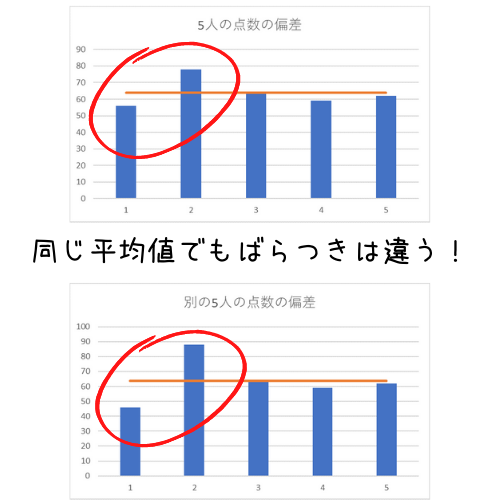
平均値で大まかなデータの全体像をみて、標準偏差で各データのばらつきをみる組み合わせで、かなり得られる情報量が増えますよ。
正規分布前提なら、平均±1×標準偏差内に収まる確率が68％とかあるけどまた後日
・標準偏差の値が小さい方がデータのばらつきも小さい
基本的にどんな値にも言えることですが、元のデータ数が少ない時は数値が雑になるので、調査対象は多めにとりましょうね。
おわりに：平均＋標準偏差のダブル使いで情報を読み取ろう！
統計は、「統計」という言葉や細かい数式のせいで苦手意識や拒否反応が出やすい分野です。
もちろん内容をきちんと理解できるに越したことはありませんが、
② SDなど略語を知る
③ それぞれを求めることで何を知れるか
①～③を大まかに理解できるだけでも十分だったりします。
今回は本当に最低限の内容だからまず見てみて！
基本的には平均値で全データを大まかに把握して、標準偏差（SD）で個々のデータのばらつきをみることでかなりの情報を集めることができま。
〇全部のデータを含めたおおよその中心値を知れる
△極端な値（外れ値）の影響を受けやすい
△同じ平均値でも中身のデータのばらつきは様々
〇全データの個々のばらつきをみることができる
◎統計的仮説検定（心理の卒論）と相性抜群
△計算につまずく人多数
また、今回紹介した偏差と分散は統計の読み取りであまり使われませんが、標準偏差を理解するために「ふーん」くらいで知っておけると便利です。
ふーん
✓偏差…平均値からどれだけ±に離れているか
✓分散…データのばらつき
「偏差＜分散＜標準偏差」と統計処理をしやすくしたイメージ
偏差（平均とのずれ）が大きいと標準偏差も当然大きくなります。
標準偏差の値は小さい方がばらつきも小さくなるため、値としてみるなら小さい数値になっているとよさげかも。
標準偏差に関連する「正規分布」など他にも用語はありますが今回はここまで！
あとはおすすめ本だよ～
統計の考え方を分かりやすく知れるおすすめはこちらの文庫です。
ポチップ
文章多めの読み物ですが、たとえ話がとにかく分かりやすい！
文系で統計扱う人で統計や数字に苦手意識がある人は1度読んでみて損なしかと。
心理系大学院受験を考えている人はこちらも読んでみてください。
ポチップ
河合塾KALSシリーズはどれも見やすくとっつきやすいのがおすすめポイント。
同シリーズの参考書はどれもキーワードがまとまっていてインプットに最適なので迷ったら購入してみてください。
コメント